photo&lyric by ｓｏｒａ (@Skylit_Blue)
おはようTwitter

きょうも
希望の二文字を心に添えて ໒꒱⋆ﾟ

◯ 公認臨床対策統計はやっぱりやっとうけい

1.独立変数と従属変数

独立変数というのは原因、従属変数というのは結果。実験計画で使われる仮説検定のための概念

例：独立変数＝新薬の抗うつ剤

　　従属変数＝新薬の量の増減でどの程度患者
　　　　　　　さんの精神状態が変化するか

　　多変量解析などで使う概念
　　説明変数＝バネに吊るすおもりの重さ
　　（予測変数）
　　基準変数＝バネの伸びた長さ
　　（目的変数）

2.尺度

⑴ 名義尺度（分類のための尺度）
　　
他のものと判別するだけの尺度、A君は心理学部、Bさんは法学部、C君は経済学部等

目的は等価の決定
文学部に所属しているのはA君、D君、Eさん

可能な統計処理
最頻値（モード）・心理学部に所属している学生が一番多い。χ二乗検定（質的検定なので可能）ノンパラメトリック（正規分布に従わない）検定

尺度の変換は1対1置換
例：西武高橋の背番号は13

⑵ 順序尺度

例：マラソンの順位

1位と2位、3位のタイムの差が5秒だろうが1分だろうが気にしない。順序のみを見る。

可能な統計処理
ア　順序を並べた際の中央値→メディアン

イ　四分位偏差＝Q（公認心理師試験既出）
　　0,1,/3,3/4,5,/6,6
　　四分位に25パーセントずつ数列を分ける
　と/の前後の平均が取れる。
　Q1は1+3/2＝2,Me（中央値）は3+4/2＝　　
　3.5、Q2は5+6/2＝5.5
（四分位偏差図）



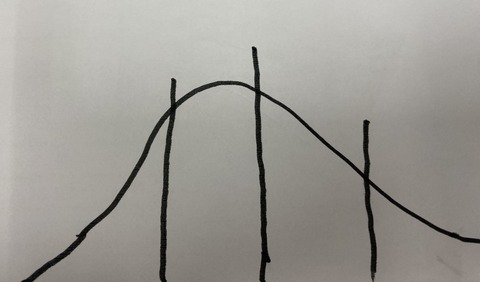
ウ　順位相関係数
　　最も簡単に言えば2つの数の間に相関があ
　るか。

エ　マン・ホイットニーの検定（母集団同士が
　同じ【何の差もないという帰無仮説】）
　
オ　符合つき順位和検定
　　母集団間の検定

尺度の変換
単調増加または減少変換
（単調にただ増え続けていくか、減少するか）　　

※ 以上名義尺度と順序尺度は質的尺度です。

⑶ 間隔尺度（距離尺度）
例：温度・温度は通常使われる温度表記10℃と20℃とは数値にすると2倍。しかし温度は絶対零度が −273.15 ℃
が原点なので2倍にはならない。順位のほかに等間隔や間隔の広がりが示されている。

可能な統計処理

算術平均
標準偏差（SD）
ピアソンの相関係数
t検定
分散分析等

尺度の変換は1次変換
Y＝aX+b

⑷ 比率尺度（比例尺度）

間隔尺度と違って原点があります。

おもりの重さ、棒の長さは絶対値が決まっていて、0からスタートして1キログラムと10キログラムの比率、15センチと30センチの差が見られます。

比例変換はあらゆる統計的処理が可能です。
尺度変換は比例なのでY＝aXです。

※ 尺度の部分についてはほぼほぼ福村出版の図表を引用しながら自分で調べ、心理統計の全くの初心者にも理解しやすいように加除しながら書いております。僕の解釈が間違っていた場合にはわかりやすく、心理統計の初心者でも読解できる、僕がtweetでつぶやき続けている名著「あなたもできる データの処理と解析」福村出版の原典を参考にしてください。公認心理師試験に十分対応できると思います。　

福村出版@fukumurashuppan
↑心理書籍を出している福村出版さんのTwitterアカウント

◯ さて、間隔尺度の「可能な統計処理」に出てきた概念について説明しておきます。どれも重要な概念です。

算数のテストをA、B、Cさんが受けました。
それぞれの点数はAさん＝61点、Bさん＝70点、Cさん＝79点でした。
算術平均点は（61＋70＋79）÷3＝70点でした。

偏差というのは平均との差です。Aさんの偏差＝ー9、Bさん＝0、Cさん+9です。

偏差を二乗します。Aさん81、Bさん0、Cさん81です。この偏差二乗の数値3人分の平均を求めます。（81+0+81）÷3＝54で、この54という数値が、ばらつき具合を見る「分散」です。分散の平方根が標準偏差です。標準偏差は7.35です。標準偏差（SD）もデータのちらばり具合を見ます。この標準偏差で偏差値が求めることができます。

さて、次にピアソンの相関係数です。
ピアソンの相関係数はエクセルでも求められるので、詳しい式は割愛しますが、相関は-1から+1の間を取ります。1に近いほど相関が強く、負の相関は逆です。煙草を1日25本以上に吸う人のCOPDが高く0.80の場合には強い相関があると言えます。飴を好きな人がCOPDになる相関は関係していないので0です。

t 検定
さきほどノンパラメトリックについて述べましたが、パラメトリックとは正規分布のことを言います。成長期にある子どもの身長は一人一人はバラバラでも図表にしてみると正規分布になります。
（正規分布の図）



t検定はパラメトリックな検定で、「帰無仮説」（差がないこと）を仮定して行い、この仮説が棄却されるかどうかを見ます。例えばさきほどの身長の例で言うと「10歳男子と15歳男子の身長には差がない」と仮定してt 検定を行うわけです。

分散分析はANOVAはt 検定が2つの母集団分析なのに対し、母集団数が3つ以上になると煩雑になるので分散分析です。さきほどの10歳男子、15歳、17歳でその差を見るというのは一元配置です。

それに加えて体重をそれぞれ加えると複雑になり二元配置になります。

1日に摂取するカロリー量や運動量を加えていくと多元配置になります。

Y＝a X+bは中学で習った「／」のような直線式です。

統計の中で尺度というのはかなり重要な概念です。

※ アナウンス

従来の「公認心理師試験」カテゴリを
公認心理師試験対策 と
公認心理師試験制度 に分割しました。

青字クリックで飛びます。
Tweet